Tukey vs. Student

Abstract

To compare two samples, or groups, we can use a T-test. But if we want to compare more than two groups, we need to use Tukey’s test. In this post we investigate the reason why a Tukey’s test is more appropriate and robust than a set of pairwise T-tests for all possible combinations of groups. This is also an excuse to illustrate the power of purrr and dplyr packages, specifically for the use of map/reduce, join_left, and pivot_longer/pivot_wider functions.

Packages that we need

In this example, we are using the packages tidyverse and adas.utils version 1.1.4 (see https://github.com/pbosetti/adas.utils)

library(tidyverse)
library(adas.utils)

Repeated T-test vs. Tukey’s test

The dataset

Let us compare the result of a Tukey’s test with a repeated Student’s T-test on all combinations. We consider the cotton dataset, which is included in the adas.utils package from version 1.1.4. The dataset contains the tensile strength of mixed cotton-synthetic yarns with different cotton content:

cotton %>% 
  ggplot(aes(x=Cotton, y=Strength, group=Cotton)) +
  geom_boxplot()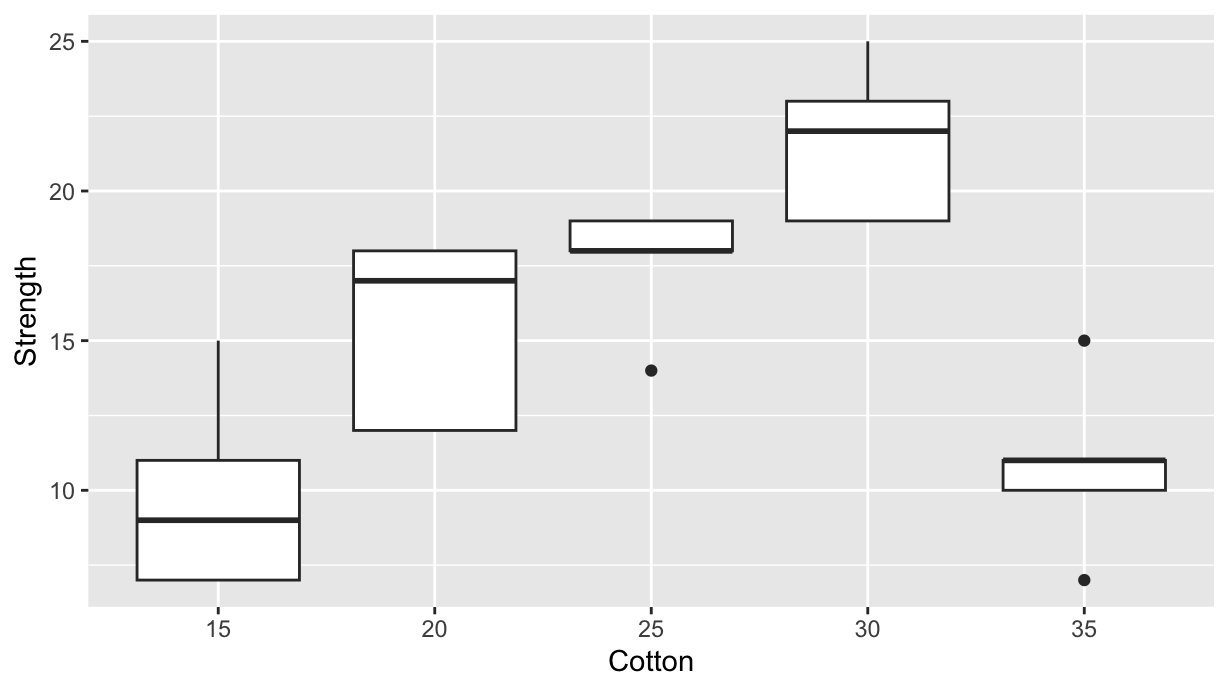

Inference on Strength

Now we want to compare all the possibile combinations of treatmentswith a set of pairwise T-tests.

First, we create the list of pairwise combinations, sorting each pair in descending order, as it is done by the TukeyHSD function:

lvl <- levels(cotton$Cotton) %>% 
  combn(2, FUN=sort, decreasing=T) %>% 
  as_tibble(.name_repair="minimal") %>% 
  as.list() %>% glimpse()

List of 10
 $ : chr [1:2] "20" "15"
 $ : chr [1:2] "25" "15"
 $ : chr [1:2] "30" "15"
 $ : chr [1:2] "35" "15"
 $ : chr [1:2] "25" "20"
 $ : chr [1:2] "30" "20"
 $ : chr [1:2] "35" "20"
 $ : chr [1:2] "30" "25"
 $ : chr [1:2] "35" "25"
 $ : chr [1:2] "35" "30"

Now, for each pair we do a T-test on the corresponding cotton data-frame subset, and accumulate into a new tibble the values of interest. We get the df table that is analogous to the TukeyHSD output:

df <- lvl %>% reduce(\(acc, pair) {
  tt <- cotton %>% 
    filter(Cotton %in% pair) %>% 
    t.test(Strength~Cotton, data=., var.equal=TRUE)
  bind_rows(acc, list(
    pair = paste0(pair[1], "-", pair[2]),
    diff = -median(tt$conf.int),
    lwr = -tt$conf.int[2],
    upr = -tt$conf.int[1],
    p.value = tt$p.value
  ))
}, .init=tibble()) 

df %>% knitr::kable()

pair	diff	lwr	upr	p.value
20-15	5.6	0.8740978	10.3259022	0.0257453
25-15	7.8	3.7398608	11.8601392	0.0021967
30-15	11.8	7.4246648	16.1753352	0.0002541
35-15	1.0	-3.5423014	5.5423014	0.6253800
25-20	2.2	-1.6724395	6.0724395	0.2265324
30-20	6.2	1.9982605	10.4017395	0.0093233
35-20	-4.6	-8.9753352	-0.2246648	0.0415629
30-25	4.0	0.5641312	7.4358688	0.0277266
35-25	-6.8	-10.4461127	-3.1538873	0.0026133
35-30	-10.8	-14.7941163	-6.8058837	0.0002496

To be compared with Tukey’s values:

ttdf <- TukeyHSD(aov(lm(Strength~Cotton, data=cotton)))$Cotton %>% 
  as.data.frame() %>% 
  rownames_to_column(var="pair") %>% 
  rename(p.value=`p adj`)
ttdf %>% knitr::kable()

pair	diff	lwr	upr	p.value
20-15	5.6	0.2270417	10.9729583	0.0385024
25-15	7.8	2.4270417	13.1729583	0.0025948
30-15	11.8	6.4270417	17.1729583	0.0000190
35-15	1.0	-4.3729583	6.3729583	0.9797709
25-20	2.2	-3.1729583	7.5729583	0.7372438
30-20	6.2	0.8270417	11.5729583	0.0188936
35-20	-4.6	-9.9729583	0.7729583	0.1162970
30-25	4.0	-1.3729583	9.3729583	0.2101089
35-25	-6.8	-12.1729583	-1.4270417	0.0090646
35-30	-10.8	-16.1729583	-5.4270417	0.0000624

Now let’s join both tables and make a common plot:

compared <- df %>% 
  left_join(ttdf, by=join_by(pair), suffix=c(".student", ".tukey")) %>% 
  pivot_longer(-pair, names_to = c("stat", "test"), names_pattern = "(.*)\\.(student|tukey)$") %>% 
  pivot_wider(names_from = stat)

compared %>% knitr::kable()

pair	test	diff	lwr	upr	p.value
20-15	student	5.6	0.8740978	10.3259022	0.0257453
20-15	tukey	5.6	0.2270417	10.9729583	0.0385024
25-15	student	7.8	3.7398608	11.8601392	0.0021967
25-15	tukey	7.8	2.4270417	13.1729583	0.0025948
30-15	student	11.8	7.4246648	16.1753352	0.0002541
30-15	tukey	11.8	6.4270417	17.1729583	0.0000190
35-15	student	1.0	-3.5423014	5.5423014	0.6253800
35-15	tukey	1.0	-4.3729583	6.3729583	0.9797709
25-20	student	2.2	-1.6724395	6.0724395	0.2265324
25-20	tukey	2.2	-3.1729583	7.5729583	0.7372438
30-20	student	6.2	1.9982605	10.4017395	0.0093233
30-20	tukey	6.2	0.8270417	11.5729583	0.0188936
35-20	student	-4.6	-8.9753352	-0.2246648	0.0415629
35-20	tukey	-4.6	-9.9729583	0.7729583	0.1162970
30-25	student	4.0	0.5641312	7.4358688	0.0277266
30-25	tukey	4.0	-1.3729583	9.3729583	0.2101089
35-25	student	-6.8	-10.4461127	-3.1538873	0.0026133
35-25	tukey	-6.8	-12.1729583	-1.4270417	0.0090646
35-30	student	-10.8	-14.7941163	-6.8058837	0.0002496
35-30	tukey	-10.8	-16.1729583	-5.4270417	0.0000624

compared %>%
  ggplot(aes(x=diff, y=pair, color=test)) + 
  geom_point() + 
  geom_errorbar(aes(xmin=lwr, xmax=upr), width=0.5, position=position_dodge()) + 
  geom_vline(xintercept=0, color="red") +
  labs(x="Difference", y="Pair", title="95% pairwise confidence level")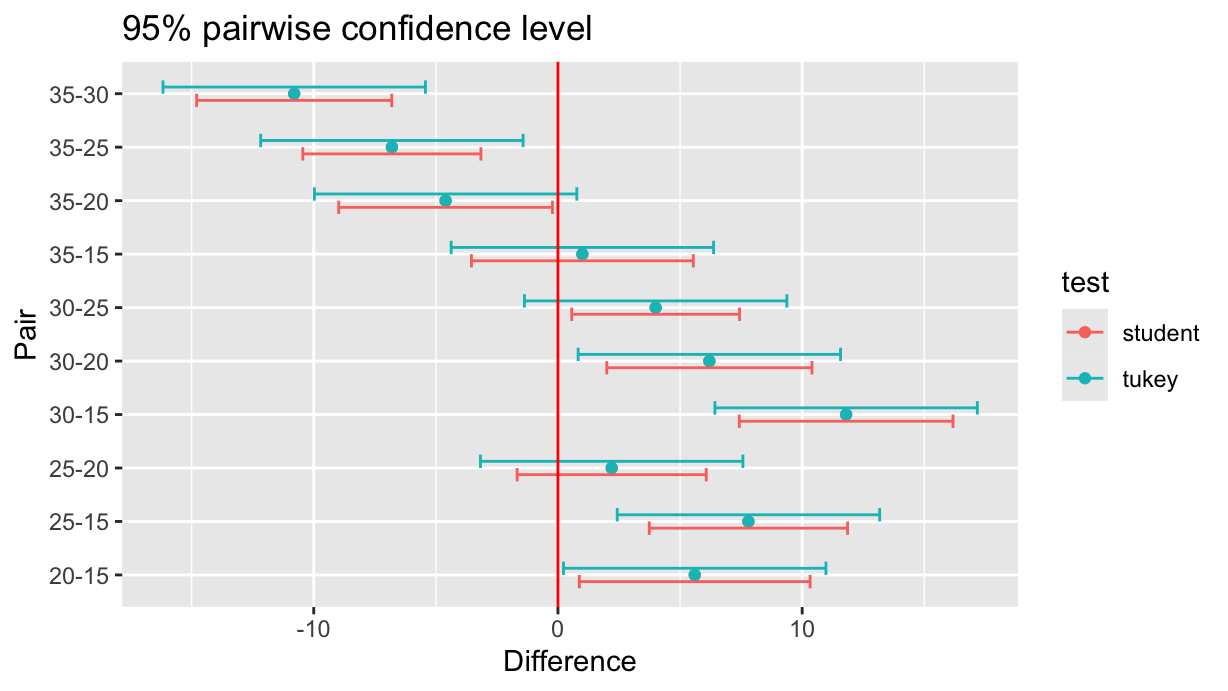

The Family-Wise Error Rate

The Family-Wise Error Rate

As expected, the Tukey’s test in the last plot shows larger confidence intervals, that is, it has reduced chances of a false positive (Type I Error). More specifically, Tukey’s test controls the family-wise error rate (FWER) — the probability of making any false positive in the full set of comparisons.

Let’s see why. If we set a confidence level of 0.95, it means that the probability of not making a Type I error on a single T-test is 0.95.

For 3 independent tests, the probability of no Type I error at all (in any of the tests) is: \[ 0.95^3 \approx 0.857 \] So the chance of making at least one Type I error is: \[ 1 - 0.95^3 \approx 0.143 \quad \text{(14.3\%)} \] That’s almost triple the risk you thought you were accepting! Furthermore, this risk increases exponentially with the number of comparisons. Given \(n\) elements, the number of possible combinations of \(k\) elements is given by the binomial coefficient: \[ \binom{n}{k} = \frac{n!}{k!(n-k)!} \] In R, the latter is provided by the choose(n, k) function:

choose(5, 2)

[1] 10

so, with increasing number of classes to be compared, this is what happens to the probability of committing at least one Type-I error:

2:15 %>% reduce(\(acc, k) {
    nt <- choose(k, 2)
    bind_rows(acc,
      list(n=k, p=1-0.95^nt)
    )
  }, .init=tibble()) %>% 
  ggplot(aes(x=n, y=p)) +
  geom_point() +
  geom_line() +
  ylim(0, 1) +
  labs(
    x="number of classes", 
    y="probability of Type-I Error")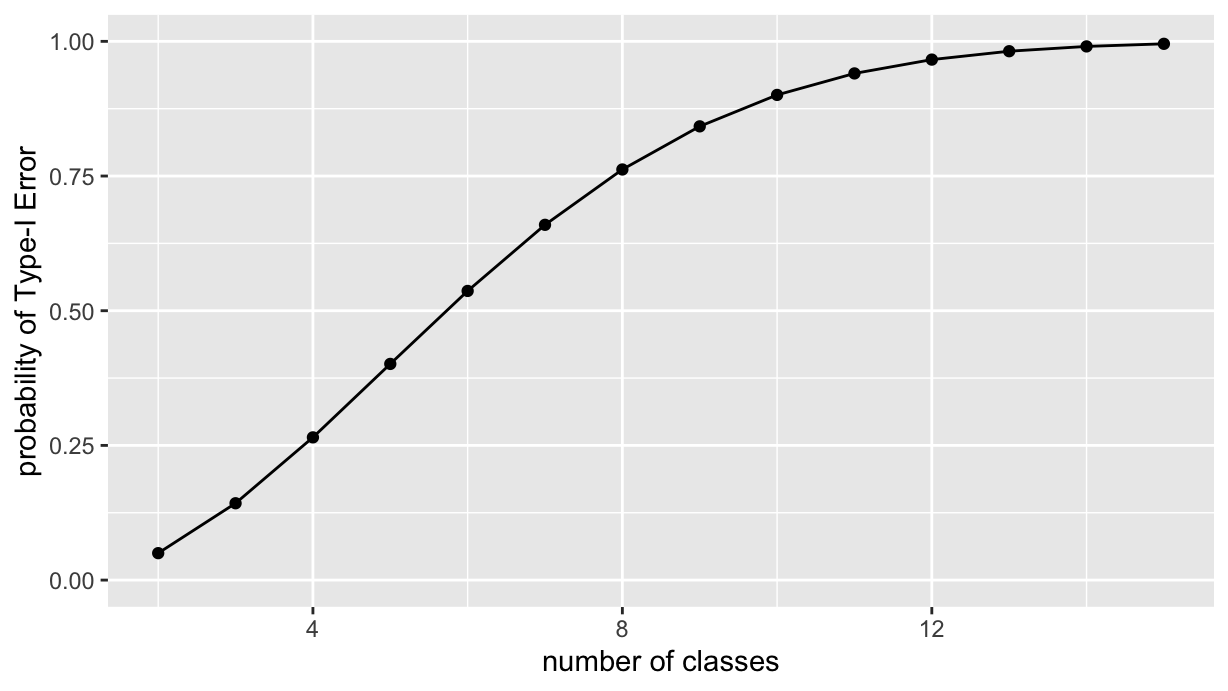

And what happens if we change the confidence level? Let’s see, by creating a parametric plot similar to the ast one, but with different confidence levels. First we factor the last reduce opration into a function, FWER, that takes the confidence level as an argument. The function returns a tibble with the number of classes and the corresponding probability of Type I error.

FWER <- function(levels, conf.int=0.95) {
  reduce(levels, \(acc, k) {
    nt <- choose(k, 2)
    bind_rows(acc,
      list(n=k, p=1-conf.int^nt)
    )
  }, .init=tibble()) 
}

Then we apply the FWER function to a set of confidence levels, and join the results into a single tibble via the usual reduce, and finally, we plot the results:

cl <- c(0.9, 0.95, 0.99, 0.995, 0.999) 
N <- 2:15
cl %>% 
  reduce(\(acc, ci) {
    fwer <- FWER(N, ci) %>% rename(!!paste0("cl-", ci):=p)
    left_join(acc, fwer, by=join_by(n))
  }, .init=tibble(n=N)) %>% 
  pivot_longer(-n, names_to = c(NA, "cl"), names_pattern="(cl-)(.*)") %>% 
  ggplot(aes(x=n, y=value, color=cl)) + 
  geom_point() + 
  geom_line() + 
  ylim(0, 1) + 
  labs(
    x="number of classes", 
    y="probability of Type-I Error", 
    color="Conf. level")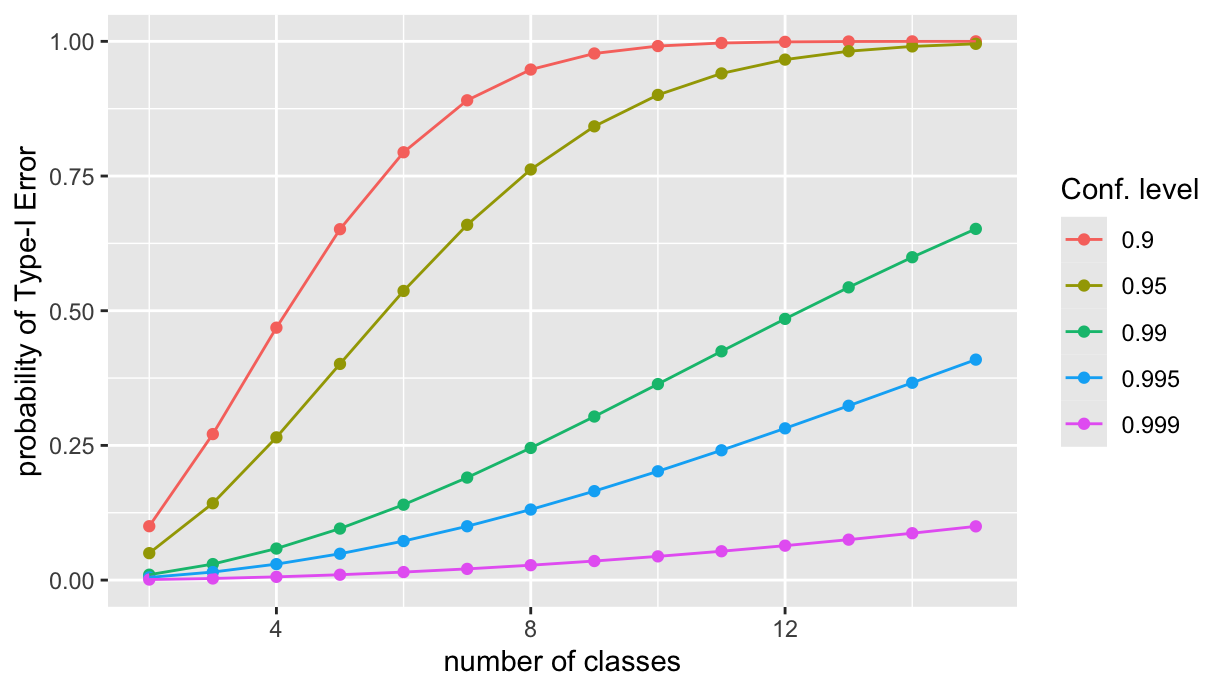

That’s all, folks!